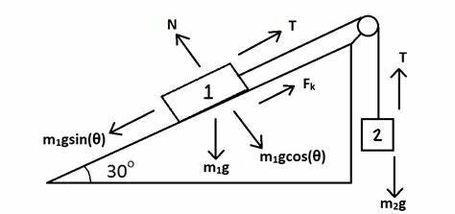
A free body tension pulley is a system that involves a rope or cable passing over a pulley and connecting two or more objects. The tension force in the rope or cable is the same throughout the system, and it causes the objects to accelerate or remain in equilibrium. To analyze a free body tension pulley system, we need to draw a free-body diagram for each object, showing all the forces acting on it. These forces include the weight of the object, the tension force in the rope or cable, and any external forces such as friction or air resistance. Then, we can apply Newton’s second law of motion to each object and write down the equations based on the forces. By solving these equations, we can find the tension force and the acceleration of the objects.
Here is an example of a free body tension pulley system and how to solve it:
In this system, two masses, m1 and m2, are connected by a rope passing over a pulley. The system is frictionless, and the pulley is massless. We want to find the tension force in the rope and the acceleration of the masses.
tep 1: Draw a free-body diagram for each mass, showing the forces acting on it. For m1, the forces are the weight (m1 * g) and the tension (T). For m2, the forces are the weight (m2 * g) and the tension (T).
tep 2: Apply Newton’s second law of motion to each mass. For m1, the net force is equal to the mass times the acceleration:
$$T – m_1g = m_1a$$
For m2, the net force is equal to the mass times the acceleration:
$$m_2g – T = m_2a$$
tep 3: Solve the equations for the tension and the acceleration. We can add the two equations to eliminate the tension:
$$(m_1 + m_2)g – 2T = (m_1 + m_2)a$$
$$2T = (m_1 + m_2)g – (m_1 + m_2)a$$
$$T = frac{(m_1 + m_2)g – (m_1 + m_2)a}{2}$$
We can substitute this expression for T into one of the equations to find the acceleration:
$$
Free Body Diagram Tension Pulley image
