Argand was a Swiss amateur mathematician who lived in the late 18th and early 19th centuries. He is best known for his contributions to the field of complex analysis, especially the geometric representation of complex numbers and the proof of the fundamental theorem of algebra.
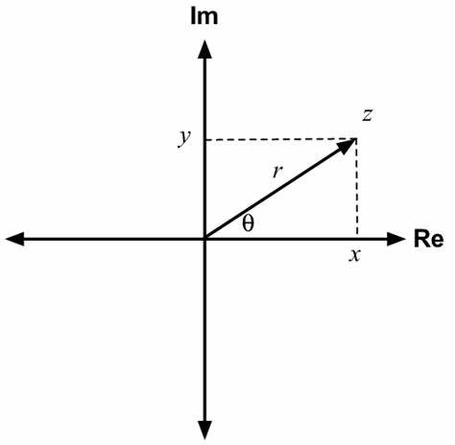
Complex numbers are numbers of the form x + iy, where x and y are real numbers and i is the imaginary unit, defined by i^2 = -1. Argand realized that complex numbers can be visualized as points on a plane, where the horizontal axis is the real part and the vertical axis is the imaginary part. This plane is now called the Argand plane or the complex plane. On this plane, complex numbers can be expressed in polar coordinates as well, using the modulus (or absolute value) and the argument (or angle) of the complex number. Argand also introduced the notation for the modulus of a complex number, denoted by |z|, and the concept of vectors, which are directed line segments that represent complex numbers.
Argand also provided the first rigorous proof of the fundamental theorem of algebra, which states that every polynomial equation with complex coefficients has at least one complex root. His proof was based on the idea of winding numbers, which count how many times a curve winds around a point. He showed that if a polynomial has no roots, then its winding number around any point is zero, which leads to a contradiction. His proof was published in 1814, but it was not widely recognized until later, when it was reproduced by Cauchy and Chrystal in their textbooks.
Argand was not a professional mathematician, but rather a self-taught enthusiast who pursued mathematics as a hobby. He worked as a bookshop manager in Paris, where he published his works privately or in journals. He died in
