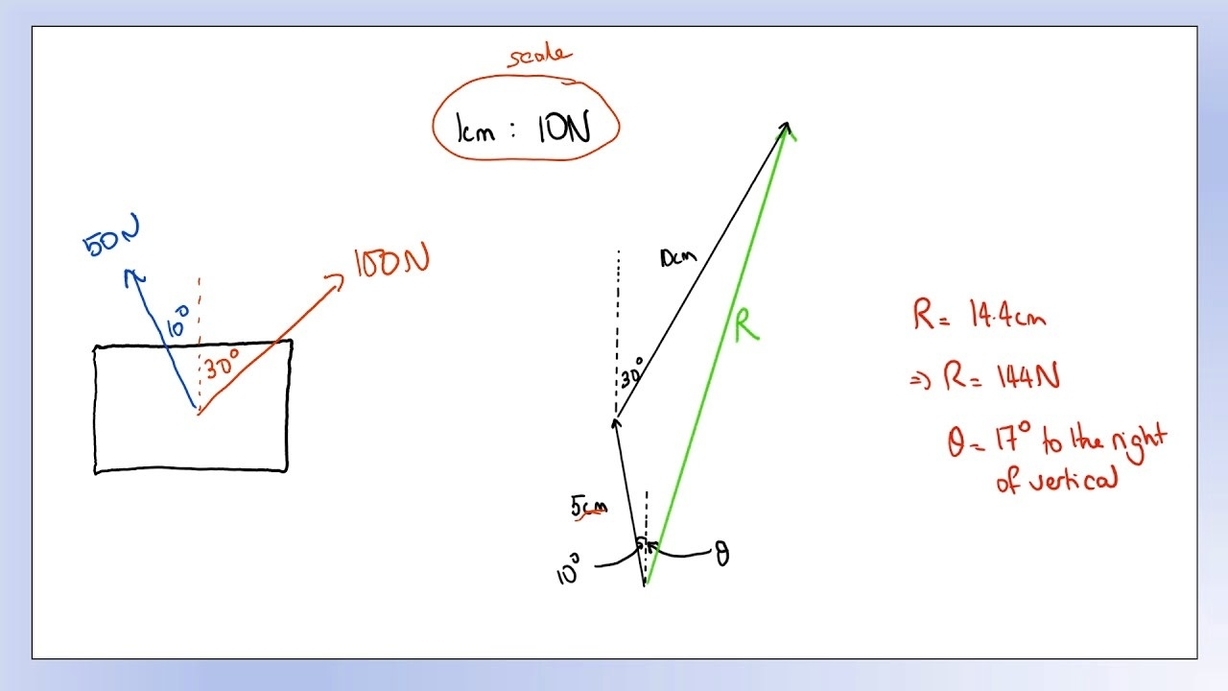
Vector addition is a fundamental operation in mathematics and physics. It is used to combine two or more vectors into a single vector. In two dimensions, vectors are represented as arrows with a magnitude and direction. The magnitude of a vector represents its length, while the direction represents the angle between the vector and the positive x-axis.
To add two vectors in two dimensions, we can use the parallelogram rule or the head-to-tail method. The parallelogram rule involves drawing the two vectors as adjacent sides of a parallelogram. The diagonal of the parallelogram represents the sum of the two vectors. The head-to-tail method involves placing the tail of one vector at the head of the other vector. The sum of the two vectors is the vector that starts at the tail of the first vector and ends at the head of the second vector.
The vector addition formula in two dimensions is as follows: (a,b) + (d,e) = (a + d, b + e). This means that to add two vectors, we simply add their corresponding components. For example, if we have two vectors v1 = (2,3) and v2 = (4,1), then their sum is v1 + v2 = (2 + 4, 3 + 1) = (6,4).
We can also subtract two vectors using the same formula. To subtract vector v2 from vector v1, we simply add the opposite of v2 to v1. The opposite of a vector is a vector with the same magnitude but opposite direction. For example, if we have two vectors v1 = (2,3) and v2 = (4,1), then v1 – v2 = v1 + (-v2) = (2,3) + (-4,-1) = (-2,2).
In summary, vector addition is a fundamental operation in mathematics and physics. In two dimensions, vectors are represented as arrows with a magnitude and direction. To add two vectors, we can use the parallelogram rule or the head-to-tail method
Vector Addition In Two Dimension image
