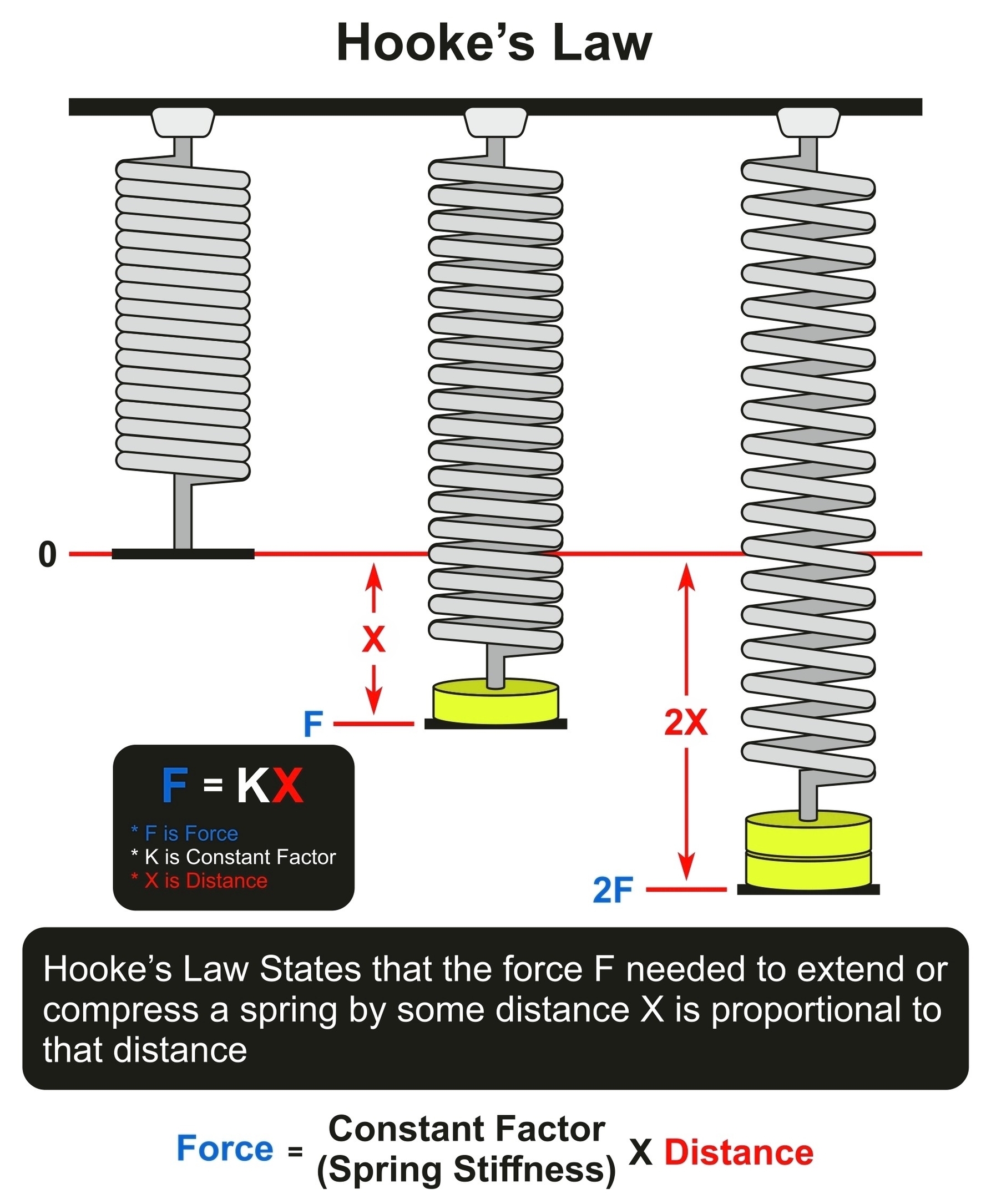
Spring constant is a measure of the stiffness of a spring or an elastic material. It tells you how much force you need to apply to stretch or compress the spring by a certain distance. The spring constant is denoted by the symbol k and has the unit of newtons per meter (N/m).
The spring constant is related to the restoring force of the spring by Hooke’s law, which states that the force is proportional to the displacement of the spring from its equilibrium position. The formula for Hooke’s law is:
$$F = -kx$$
where F is the restoring force, x is the displacement, and k is the spring constant. The negative sign indicates that the force is opposite to the direction of the displacement.
The spring constant depends on the properties of the spring, such as its material, shape, and size. Different springs have different spring constants, and the larger the spring constant, the stiffer the spring. For example, a spring with a spring constant of 100 N/m is stiffer than a spring with a spring constant of 50 N/m.
The spring constant can be calculated by measuring the force and the displacement of the spring and using Hooke’s law. For example, if a spring is stretched by 0.2 m when a force of 10 N is applied, then the spring constant is:
$$k = frac{F}{x} = frac{10}{0.2} = 50 text{ N/m}$$
The spring constant can also be derived from the physical characteristics of the spring, such as its length, cross-sectional area, and Young’s modulus. Young’s modulus is a measure of the elasticity of a material, and it is defined as the ratio of stress to strain. The formula for the spring constant in terms of these parameters is:
$$k = frac{EA}{L}$$
where E is the Young’s modulus, A is the cross-sectional area, and L is the length of the spring.
The spring constant is important for understanding the behavior of springs and elastic materials in various situations, such as oscillations, vibrations, and energy storage. For example, the spring constant determines the natural frequency of a spring-mass system, which is given by:
$$f = frac{1}{2pi}sqrt{frac{k}{m}}$$
where f is the frequency, k is the spring constant, and m is the mass attached to the spring. The natural frequency is the frequency at which the system oscillates when it is displaced from its equilibrium position and released.
The spring constant also determines the elastic potential energy stored in a spring, which is given by:
$$U = frac{1}{2}k
