Month: February 2024

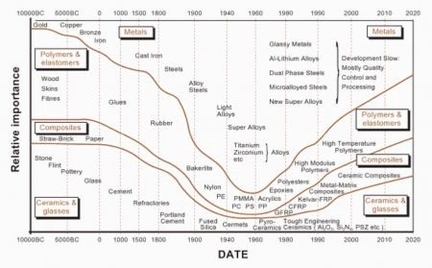
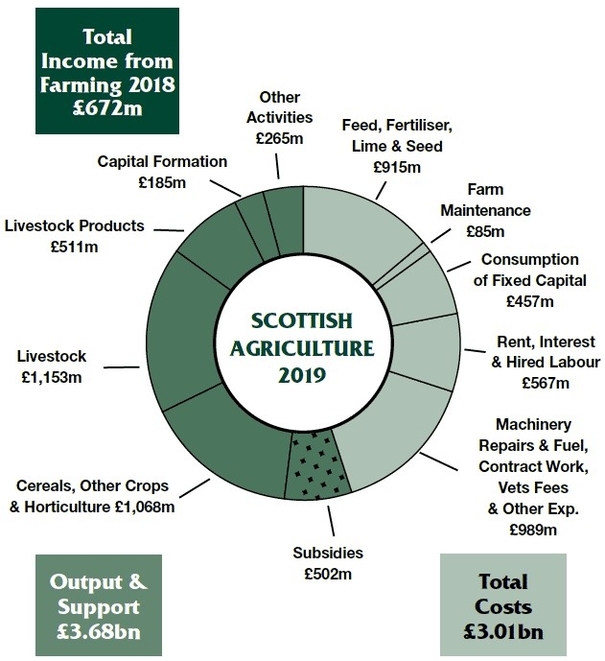
Chopped composites are a type of composite material that are made up of short fibers that are randomly oriented and held together by a matrix material. The schematic of a chopped composite is shown in the figure below.


The fibers in a chopped composite are typically made of glass, carbon, or aramid, and are usually between 0.1 and 0.5 inches in length. The matrix material can be made of a variety of materials, including thermoplastics, thermosets, and metals.

Chopped composites have a number of advantages over other types of composite materials. For example, they are relatively inexpensive to produce, and can be made in a variety of shapes and sizes. They are also lightweight and have good mechanical properties, such as high strength and stiffness.

One of the challenges with chopped composites is that the orientation of the fibers is random, which can lead to anisotropic properties. This means that the properties of the material can vary depending on the direction in which it is loaded. To overcome this challenge, researchers have developed models to predict the mechanical behavior of chopped composites.

In summary, chopped composites are a type of composite material that are made up of short fibers that are randomly oriented and held together by a matrix material. They have a number of advantages over other types of composite materials, but also present some challenges due to their anisotropic properties. Researchers have developed models to predict the mechanical behavior of chopped composites.

Life history evolution is a fascinating topic that seeks to explain how natural selection and other evolutionary forces shape organisms to optimize their survival and reproduction in the face of ecological challenges posed by the environment. Life history traits are the major components of fitness, and since adaptation by natural selection is based on variation in Darwinian fitness among individuals, understanding life history evolution is crucial to understanding adaptation, the most fundamental issue in evolutionary biology.

Life history evolution is about understanding how evolution shapes organisms to optimize their reproductive success. Organisms differ dramatically in how they develop, the time they take to grow, when they become mature, how many offspring of a particular size they produce, and how long they live. Together, the age-, size-, or stage-specific patterns of development, growth, maturation, reproduction, survival, and lifespan define an organism’s life cycle, its life history.

Life history theory seeks to explain how natural selection and other evolutionary forces shape organisms to optimize their survival and reproduction in the face of ecological challenges posed by the environment. The theory does so by analyzing the evolution of fitness components, so-called life history traits, and how they interact: size at birth; growth pattern; age and size at maturity; number, size, and sex of offspring; age-, stage- or size-specific reproductive effort; age-, stage- or size-specific rates of survival; and lifespan.

The study of life history evolution is important because it helps us understand how organisms have evolved to optimize their reproductive success in different environments. For example, a female North Pacific Giant Octopus (Enteroctopus dofleini) lives three to four years; it lays thousands of eggs in a single bout and then dies. By contrast, a mature Coast Redwood Tree (Sequoia sempervirens) lives for many hundreds of years and produces millions of seeds each year. As these two examples illustrate, organisms differ dramatically in their life histories.

Life history evolution is a complex topic, and there is still much to learn about how natural selection shapes the life histories of different organisms. However, by studying life

Uplands is a semi-private golf and ski club located in Thornhill, Ontario, Canada?. The club was designed by the legendary golf course architect, Stanley Thompson, and opened in 1922 as an eighteen-hole private course. However, due to urban sprawl, half of the course was lost in 1989, and it became a nine-hole course[^10^]. The current nine holes at Uplands Golf Club crisscross a valley filled with mature trees and forested valley[^10^]. The course is parkland-style and provides an enjoyable and challenging experience for all levels of play.

Uplands Golf & Ski Club offers a range of services and facilities to its members and visitors. The Pro Shop carries a full range of the latest equipment, apparel, shoes, and accessories at competitive prices. The club also has a full-service restaurant that specializes in creating the ideal ambiance for your celebration and is dedicated to making your event a success.

In addition to golf, Uplands also offers skiing facilities. With a vertical drop of some 100 feet and slopes of varying difficulty averaging 1,000 feet in length, Uplands is the perfect environment to learn skiing for beginners of all ages, especially for children?. The instructors are all certified and use CSIA and CASI teaching methods that effectively develop skill and confidence in the skiers and snowboarders of all ages?.

Uplands Golf & Ski Club is a vibrant and established semi-private club, and its diverse membership shares a strong foundation of social values and commitment to the community. When you join the club, you join the family. Throughout the year, Uplands gives back to the community in many different ways.

Vector addition is a fundamental operation in mathematics and physics. It is used to combine two or more vectors into a single vector. In two dimensions, vectors are represented as arrows with a magnitude and direction. The magnitude of a vector represents its length, while the direction represents the angle between the vector and the positive x-axis.

To add two vectors in two dimensions, we can use the parallelogram rule or the head-to-tail method. The parallelogram rule involves drawing the two vectors as adjacent sides of a parallelogram. The diagonal of the parallelogram represents the sum of the two vectors. The head-to-tail method involves placing the tail of one vector at the head of the other vector. The sum of the two vectors is the vector that starts at the tail of the first vector and ends at the head of the second vector.

The vector addition formula in two dimensions is as follows: (a,b) + (d,e) = (a + d, b + e). This means that to add two vectors, we simply add their corresponding components. For example, if we have two vectors v1 = (2,3) and v2 = (4,1), then their sum is v1 + v2 = (2 + 4, 3 + 1) = (6,4).

We can also subtract two vectors using the same formula. To subtract vector v2 from vector v1, we simply add the opposite of v2 to v1. The opposite of a vector is a vector with the same magnitude but opposite direction. For example, if we have two vectors v1 = (2,3) and v2 = (4,1), then v1 – v2 = v1 + (-v2) = (2,3) + (-4,-1) = (-2,2).

In summary, vector addition is a fundamental operation in mathematics and physics. In two dimensions, vectors are represented as arrows with a magnitude and direction. To add two vectors, we can use the parallelogram rule or the head-to-tail method

Agriculture is the art and science of cultivating the soil, growing crops, and raising livestock. It includes the preparation of plant and animal products for people to use and their distribution to markets. Agriculture provides most of the world’s food and fabrics. Here are some facts about agriculture in different regions and aspects:

– Canada: Only about 7 per cent of Canada’s land can be farmed. Other marginal (poorer) land can be used to ranch cattle. Aquaculture operations are found on the East and West Coasts and in the Great Lakes. Some crops such as tomatoes, cannabis and flowers are grown in greenhouses in urban centres. Canada is a top exporter of agricultural products in the world, such as canola, beef and maple syrup.
– Farming: Farming began around 10,000 B.C. during the First Agricultural Revolution, when nomadic tribes began to farm. Additionally, this is when the eight so-called “founder crops” of agriculture appeared: 1) emmer wheat, 2) einkorn wheat, 3) hulled barley, 4) peas, 5) lentils, 6) bitter vetch, 7) chickpeas, and 8) flax. The Industrial Revolution led to faster and more efficient farming technology, which helped usher in the Second Agricultural Revolution from 1700 to 1900 in developed countries. The Third Agricultural Revolution, or the Green Revolution, corresponds in the late 20th century with the exponential population growth occurring around the world. It includes biotechnology, genetic engineering, chemical fertilizers, and mass production of agricultural goods.
– Fruit: Fruit farming began sometime between 6000 and

Weather and climate are two concepts that are often confused with each other. While they are related, they are not the same thing. Weather refers to the atmospheric conditions that occur over a short period of time, usually a few hours or days. Climate, on the other hand, is the average weather conditions that occur over a long period of time, typically 30 years or more .

To help you understand the similarities and differences between weather and climate, I found an interactive Venn diagram on the Science Learning Hub website . The diagram shows that while weather and climate are related, they are not the same thing. The diagram also shows that there are some similarities between the two concepts. For example, both weather and climate can be hot or cold, and both can be wet or dry. However, there are also some important differences between the two concepts. For example, weather can change rapidly, while climate changes slowly over time.

The Venn diagram also shows that there are some things that are unique to weather and some things that are unique to climate. For example, weather can vary from day to day, while climate is more stable and changes slowly over time. Weather can also be local, meaning that it only affects a small area, while climate is regional or global, meaning that it affects a larger area. The Venn diagram also shows that there are some things that are common to both weather and climate. For example, both weather and climate can be hot or cold, and both can be wet or dry.

In summary, weather and climate are two related but distinct concepts. Weather refers to the atmospheric conditions that occur over a short period of time, while climate refers to the average weather conditions that occur over a long period of time. While there are some similarities between the two concepts, there are also some important differences. The Venn diagram I found on the Science Learning Hub website is a great tool to help you understand the similarities and differences between weather and climate ..

Stage 4 cancer is the most advanced stage of cancer, meaning that cancer has spread from the primary tumor to other parts of the body. This is also called metastatic cancer. Stage 4 cancer is not always terminal, but it usually requires more aggressive treatment and has a lower survival rate than earlier stages. The symptoms, prognosis, and treatment options depend on the type of cancer and where it has metastasized.

Here is a brief overview of stage 4 cancer in about 1000 words:
ymptoms

The symptoms of stage 4 cancer vary depending on the type of cancer and the organs or tissues affected by the metastases. Some common symptoms of metastatic cancer are:

– Shortness of breath, cough, chest pain, or coughing up blood when cancer spreads to the lungs
– Yellowing of the skin (jaundice), abdominal swelling, fluid accumulation (ascites), or pain when cancer spreads to the liver
– Severe back pain, numbness, weakness, fractures, or loss of bowel or bladder control when cancer spreads to the bones
– Headaches, dizziness, nausea, vision or speech problems, confusion, seizures, or trouble walking when cancer spreads to the brain or spinal cord
ome general symptoms of stage 4 cancer are fatigue, weakness, weight loss, loss of appetite, and pain.

Prognosis

The prognosis of stage 4 cancer depends on many factors, such as the type of cancer, the location and number of metastases, the response to treatment, the age and overall health of the person, and the genetic mutations of the cancer cells. Doctors usually use the 5-year survival rate to describe the outlook of stage 4 cancer. This is the percentage of people who live at least 5 years after being diagnosed with cancer. However, these rates are based on data from the past and may not reflect the current advances in treatment and care. Also, survival rates are averages and do not predict the outcome of each individual.

The 5-year survival rate for stage 4 cancer varies widely depending on the type of cancer. For example, according to the American Cancer Society, the 5-year survival rate for stage 4 breast cancer is 28%, for stage 4 prostate cancer is 32%, for stage 4 mesothelioma is

Vector addition is a fundamental operation in linear algebra that involves adding two or more vectors together to obtain a resultant vector. It is used to describe the motion of objects in space, forces acting on objects, and many other physical phenomena.

Vectors are mathematical objects that have both magnitude and direction. They can be represented graphically as arrows, where the length of the arrow represents the magnitude of the vector and the direction of the arrow represents the direction of the vector. Vector addition is the process of adding two or more vectors together to obtain a new vector that represents the sum of the original vectors.

There are two methods for adding vectors: algebraically and graphically. Algebraic addition involves adding the corresponding components of the vectors together. For example, if we have two vectors A and B, with components (a1, a2, a3) and (b1, b2, b3), respectively, then the sum of the two vectors is (a1+b1, a2+b2, a3+b3). Graphical addition involves placing the tail of one vector at the head of the other vector and drawing the resultant vector from the tail of the first vector to the head of the second vector. The resultant vector is the vector that connects the tail of the first vector to the head of the second vector.

Vector addition has several important properties. First, it is commutative, which means that the order in which the vectors are added does not matter. That is, A + B = B + A. Second, it is associative, which means that the way in which the vectors are grouped does not matter. That is, (A + B) + C = A + (B + C). Finally, it is distributive, which means that scalar multiplication can be distributed over vector addition. That is, a(A + B) = aA + aB, where a is a scalar.

Vector addition is used in many areas of science and engineering. For example, it is used to describe the motion of objects in space, such as the motion of planets around the sun. It is also used to describe the forces acting on objects, such as the forces acting on a bridge or a building.

A set is a collection of distinct objects, which can be anything from numbers to colors to people. Sets are usually denoted by capital letters, and their elements are enclosed in curly braces. For example, the set of all even numbers can be written as {2, 4, 6, 8, …}, while the set of primary colors can be written as {red, blue, yellow}.
ets can be combined using various operations, such as union, intersection, and complement. The union of two sets A and B is the set of all elements that belong to either A or B (or both), and is denoted by A ? B. The intersection of two sets A and B is the set of all elements that belong to both A and B, and is denoted by A ? B. The complement of a set A is the set of all elements that do not belong to A, and is denoted by A’.

Venn diagrams are a useful tool for visualizing sets and their relationships. A Venn diagram consists of one or more circles, each representing a set, and the area inside the circle represents the elements of the set. The circles can overlap, and the overlapping region represents the elements that belong to both sets. For example, if we have two sets A and B, we can draw a Venn diagram with two circles, one for A and one for B, and the overlapping region represents the elements that belong to both A and B.

Venn diagrams can be used to illustrate various set operations. For example, the union of two sets A and B can be represented by the entire area inside both circles, while the intersection of A and B can be represented by the overlapping region. The complement of a set A can be represented by the area outside the circle representing A.