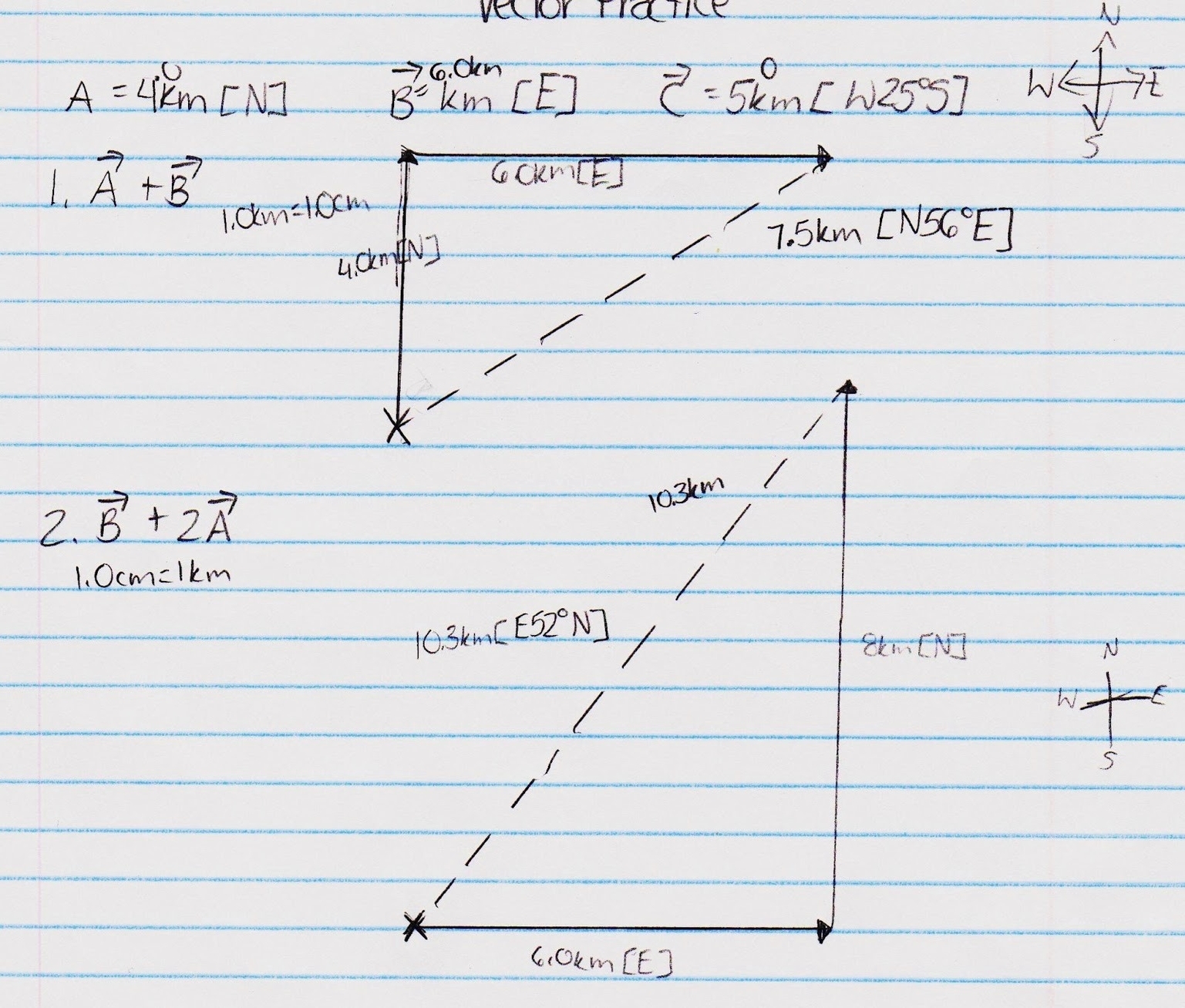
Vector addition is a fundamental operation in linear algebra that involves adding two or more vectors together to obtain a resultant vector. It is used to describe the motion of objects in space, forces acting on objects, and many other physical phenomena.
Vectors are mathematical objects that have both magnitude and direction. They can be represented graphically as arrows, where the length of the arrow represents the magnitude of the vector and the direction of the arrow represents the direction of the vector. Vector addition is the process of adding two or more vectors together to obtain a new vector that represents the sum of the original vectors.
There are two methods for adding vectors: algebraically and graphically. Algebraic addition involves adding the corresponding components of the vectors together. For example, if we have two vectors A and B, with components (a1, a2, a3) and (b1, b2, b3), respectively, then the sum of the two vectors is (a1+b1, a2+b2, a3+b3). Graphical addition involves placing the tail of one vector at the head of the other vector and drawing the resultant vector from the tail of the first vector to the head of the second vector. The resultant vector is the vector that connects the tail of the first vector to the head of the second vector.
Vector addition has several important properties. First, it is commutative, which means that the order in which the vectors are added does not matter. That is, A + B = B + A. Second, it is associative, which means that the way in which the vectors are grouped does not matter. That is, (A + B) + C = A + (B + C). Finally, it is distributive, which means that scalar multiplication can be distributed over vector addition. That is, a(A + B) = aA + aB, where a is a scalar.
Vector addition is used in many areas of science and engineering. For example, it is used to describe the motion of objects in space, such as the motion of planets around the sun. It is also used to describe the forces acting on objects, such as the forces acting on a bridge or a building.
