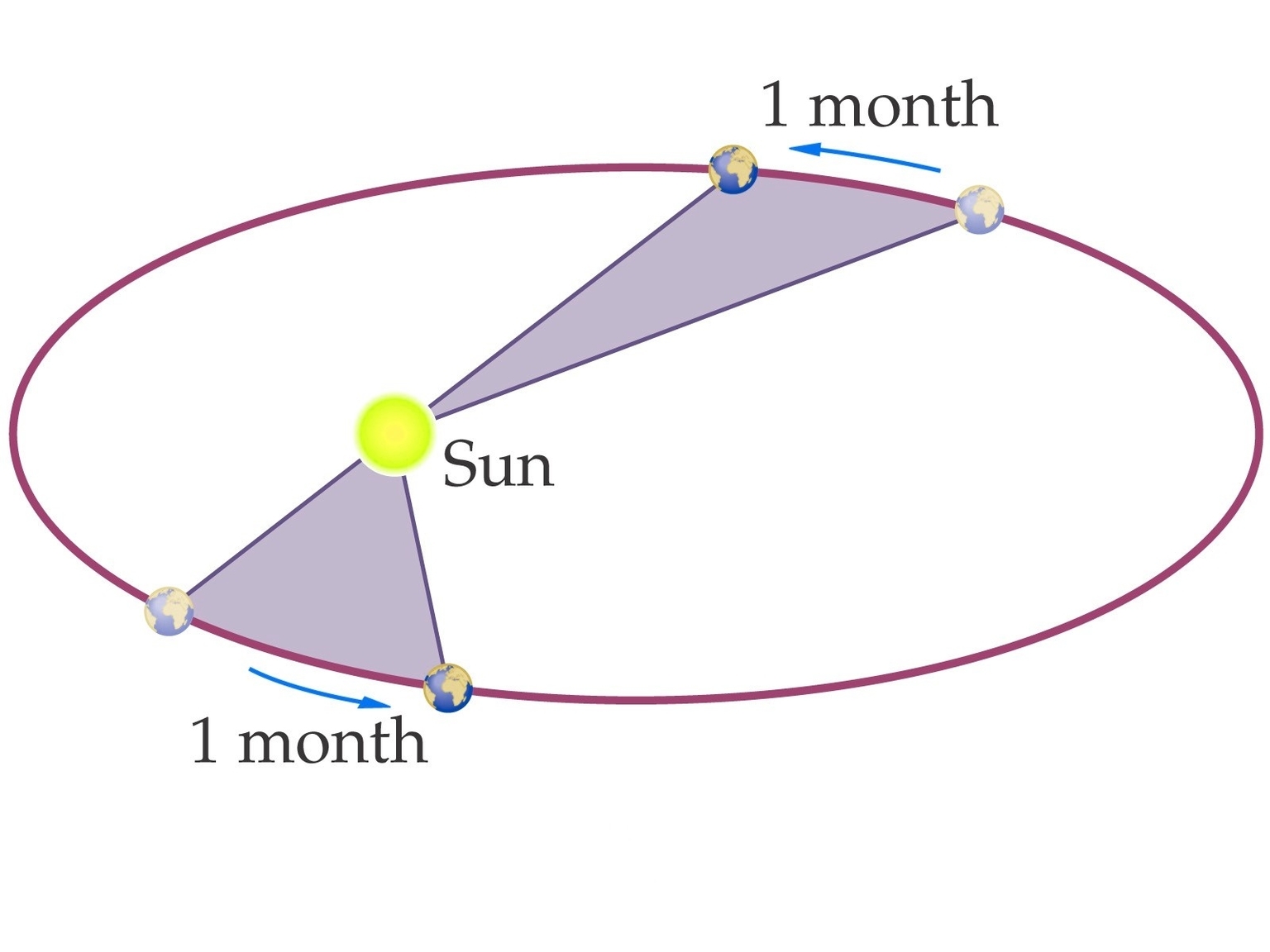
Kepler’s Second Law of Planetary Motion is one of three laws that describe the motion of planets in the solar system. It states that a radius vector joining any planet to the Sun sweeps out equal areas in equal lengths of time. This means that a planet moves faster when it is closer to the Sun and slower when it is farther away. The law is also known as the “law of areas.”
The law was derived by Johannes Kepler, a German astronomer, in the early 17th century. Kepler’s analysis of the observations of the Danish astronomer Tycho Brahe enabled him to announce his first two laws in 1609 and a third law nearly a decade later, in 1618. Kepler himself never numbered these laws or specially distinguished them from his other discoveries.
Kepler’s Second Law is a consequence of the conservation of angular momentum. Angular momentum is a measure of the amount of rotation an object has. When a planet is closer to the Sun, it moves faster because it is subject to a stronger gravitational force. This increased speed compensates for the shorter distance the planet travels in a given time, so that the area swept out by the radius vector is the same as when the planet is farther away. Conversely, when a planet is farther away from the Sun, it moves more slowly because the gravitational force is weaker. This slower speed compensates for the longer distance the planet travels in a given time, so that the area swept out by the radius vector is still the same.
Kepler’s Second Law is important because it helps explain why planets move in elliptical orbits around the Sun. An ellipse is a geometric shape that looks like a stretched-out circle. The Sun is located at one of the two foci of the ellipse. When a planet is closer to the Sun, it moves faster and sweeps out a larger area in a given time. When it is farther away, it moves more slowly and sweeps out a smaller area. This means that the planet spends more time in the parts of its orbit that are farther from the Sun, and less
